( Blog Arşiv )
- Cavendish analizi ile modern analizin farkı.
- Cavendish analizinde sarkacın dönemi. Deney sırasında Cavendish sarkacın dönemi N'yi saat tutarak hesaplıyor, analiz içinde ise teorik olarak hesaplıyor. Cavendish zamanında kronometreler, bildiğim kadar daha yeni yeni, geliştiriliyordu, acaba Cavendish bir saniye sarkacı mı kullanıyor, dönemi hesaplamak için?
- Cavendish dünyanın yoğunluğunu hesapladığını söylüyor ama dünyanın yoğunluğundan ne anladığını söylemiyor.
- Cavendish, Newton kültü ve yoğunluk ile ilgili bir yazı.
- Newtoncular Kepler Kuralını Newton markalı sembollerle yazıyorlar, artık bu çok açık olarak görülüyor. Newtoncular, Newton'un yaptıklarını harfiyen tekrarlıyorlar. Newton Kepler Kuralını \(1/R^2 = R/T^2\) olarak yazdı diye onlar da aynı şekilde yazıyorlar. Üstelik, Newton'un ölümünden sonra, Newtonculuk tam bir kült olmuş, Aristoculuk gibi, kült mensupları şeyhlerinin kutsal sözlerini tekrarlamaktan başka bir şey yapmıyorlar.
- Uydudan yoğunluk hesabına tekrar baktım, sonuç olarak, benim dediğim şeyi bir sabit ile yazıyorlar, \(\rho = K\, 1/T^2\) (\(K \equiv 3\pi/G\))
- Modern analizi de tekrarladım.
- Newton'un yörüngeyi "radyan yörüngesi" olarak tanımladığı eski yazımı da buldum, çıktı aldım, yarın okurum. Yani, \(mv^2/r\) ile yörünge hesaplanamaz.
- Yakın yörünge uydudan yoğunluk hesabına tekrar baktım, birkaç yanlış vardı onları düzelttim.
- Alternatif uydu hızı formülüne \(v' = \sqrt{\frac{GM}{R}}\) baktım, \(mv^2/r\) formülünden geliyormuş. Sorunlu, bence.
- Bu ay ne yaptım?
- Cavendish’in analizini inceledim.
- Cavendish’ten sonra geliştirilen ve modern fizik denklemleri ve birimleri ile yapılan modern analizlere de baktım
- Cavendish’in sarkacın orta noktasını ve dönemini nasıl hesapladığına baktım. Bundan sonra her deneye teker teker bakacağım.
- Deneyle ilgili sorular da var. Cavendish sarkaç kolunu hareket ettirmek için sadece telin sertliğini aşmak gerekir diyor, yani sarkaca asılı topların ağırlıksız olduğunu söylemiş oluyor, fakat daha sonra, telin geri döndürücü gücünü topun ağırlığına oranlıyor, sanki toplar ağırlıksız değilmiş gibi.
- Başka bir soru da sarkacın bu deneydeki rolü. Nasıl oluyor da bir sarkacın salınımından dünyanın yoğunluğu hesaplanabiliyor. Dünyanın yoğunluğu ağırlık ile giriyor. Sarkaç kolunu çeken kurşun ağırlığın ne kadar ağır olduğu ile dünyanın ne kadar ağır olduğu dünyanın yoğunluğunu belirliyor. Çünkü Newtoncu çekim gücü ağırlığa oranlı. Cavendish kütle kavramını kullanmıyor, sadece ağırlık kavramını kullanıyor.
- Sarkaç olmadan dünyanın yoğunluğunu hesaplayamaz mıyız? Mesela dünya yüzeyine yakın bir yörüngede olan bir uydunun döneminden dünyanın yoğunluğunu hesaplayabiliriz. [Link]
- Zaten “dünya” olarak tanımladığımız küre, insan merkezci bir tanım. İnsanların yaşadığı yarıçapın yüzeyini “dünya” gezegeni olarak tanımlamak insanları merkez alan bir düşünce tarzıdır, yani bilimsel düşünceye uygun değildir. Dünya bir yoğunluk devamlılığıdır. Kepler Kuralından her yarıçap için o yüzeyin yoğunluğu hesaplanabilir.
- Cavendish’in makalesinin önemli bölümlerini Türkçe’ye tercüme ettim.
- Cavendish deneyinde etkili olan iki güç var. Birisi telin geri döndürücü gücü bu güç tamamen mekanik bir güç, yani telin bükülmesi kolu oynatıyor, her şey mekanik yani temas ile oluyor. Diğer etkili olduğu söylenen güç de Newtoncu çekim gücü. Bu güç mekanik bir güç değil. Ağırlıkların sarkaca asılı topları çektiği söyleniyor ama bi çekimin nasıl olduğu bilinmiyor fakat kesinlikle mekanik olmadığını biliyoruz. Tanım icabı, Newtoncu güç, zaman geçmeden mesafe kateden doğa üstü veya hayali veya uydurma bir güçtür. Yani, çekim gücü uygulayan kurşun ağırlıktan çıkan Newtoncu güç, aradaki 8.85 inch mesafeyi zaman geçmeden katedip topları kendine doğru çekmektedir. Böyle sihirli bir şey nasıl oluyor bunu bilemiyoruz. Bu sebepten Cavendish deneyini aslına uygun olarak tekrarlayarak Cavendish’in gerçekten böyle bir çekim gücünü gözlemleyip gözlemlemediğini görmek istiyoruz.
- Cavendish’in analizinde gördüğüm başka bir çelişki de, Cavendish’in önce Newtoncu gücün kendini sarkacın dönemi olarak belli ettiğini söylemesi ama dünyanın yoğunluğunu hesapladığı en son formüle baktığımızda görüyoruz ki, Newtoncu güç sarkacın dönemine oranlı değil, sarkacın kolunun kayması olan B’ye oranlı.
- Diğer bir çelişki de Cavendish’in topla ağırlık arasındaki mesafeyi sabit olarak kabul etmesi. Halbuki, telin geri döndürücü gücü sarkaç kolunun döndüğü açıya oranlı olduğu halde, Newtoncu çekim gücü aradaki mesafenin karesine oranlı olduğu için bu iki gücün dengede olması söz konusu olamaz ama bütün analizler bu iki gücün dengede olması üzerine kurulmuştur.
- Bu Newtoncu çekim gücü nerede, bunu da bilemiyoruz. Newtoncu çekim gücü ağırlığa oranlı olduğu söyleniyor. Ağırlık denen şeyin nesi acaba çekim gücü olarak iş görebiliyor? Ağırlığa kütle diyerek bu gerçeği değiştiremiyorsunuz çünkü ağırlık ve kütle eşanlamlı kelimeler ikisi de hacım x yoğunluk demek.
- Modern analizler “çekim sabiti” denen G’yi temel alarak hesaplar yapılıyor.
- Bir de modern analizlerde topun kütlesi “\(m\)” olarak yazılıyor ama \(m\) sonra eleniyor. \(m\) elenince, aynı denklemde \(m\)’ye bağımlılığı olan diğer terimler anlamsız hale geliyor, mesela \(r\). \(r\) = \(M\) ile \(m\) arasındaki mesafe olduğu için, \(m\) elenince \(r\) de anlamsızlaşmış oluyor. Yani bu denklem uydurma bir fizik denklemi değil de bir bilgisayar programı olsa, bilgisayar hata verirdi, çünkü \(r\)’yi \(m\) ile tanımladınız, şimdi \(m\)’yi eleyince \(r\)’nin de anlamı kalmamış oluyor.
- Gezegene yakın dolaşan uydunun döneminden dünyanın yoğunluğunun hesaplanması.
- Cavendish'in sayıları ile "yerçekimi sabiti G". Hesapladım fakat "G"'nin bugün kabul edilen değeri çıkmadı.
- Cavendish'in sayıları ile dünyanın yoğunluğu. Cavendish bu formül ile \(D = N^2 / 10844 B\) dünyanın yoğunluğunu hesaplıyor. Çok basit. Sadece, ağırlıklar bir yakın pozisyondan diğer yakın pozisyona getirildiği deneylerde \(2B\) olduğu için, Cavendish'in verdiği \(B\)'nin yarısını kullanıyoruz.
- Cavendish'in sayılarını kullanarak \(G\) sabitini de hesaplamayı denedim ama doğru sayı çıkmadı. Bu formüle,
\(G :: 2 \,\pi^2 \,L\, r^2\, B : M \,T^2\)
Cavendish'in sayılarını koyunca "G" için kabul edilmiş sayı çıkmıyor.
- Cavendish sarkacın dönemini nasıl hesaplıyor? Çok basit, ama sarkaç kolu sabit durmadığı için, 3 uç noktanın ortalamasını alıyor.
- Modern analizi okumaya devam ettim. Cavendish'in analizi, modern analizin yanında ne kadar yalın kalıyor. Cavendish "moment of inertia" \(I\) veya "telin bükülme sabiti" \(\kappa\) gibi birim gerektiren değerlerle uğraşmıyor, her şeyi orantılarla hesaplıyor.
- Ağırlık mı, kütle mi? Cavendish kütle kavramını kullanmıyor. Modern fizikte kütle ve ağırlık tam bir ortaçağ skolastik kavram kargaşası haline getirilmiştir. Ama önemli olan Cavendish'in kütle kavramını kullanmadın dünyanın yoğunluğunu hesaplamış olmasıdır.
- Modern analize de bakıyorum. \(G\)'nin tanımında, denklemlerde \(M\) harfi ile temsil edilen sarkaca takılı topu çeken ve \(M\) harfi ile temsil edilen ağırlık ve \(m\) ve \(M\) arasındaki mesafeyi temsil eden \(r\) harfi denklemde olmakla birlikte,
\(m\) bu tanımda yok, yani \(r\) mesafesi, bu tanıma göre, \(M\) ile arasındaki mesafe, evet, cümle düşüklüğü değil bu, denklem düşüklüğü, çünkü, \(r\), iki cisim arasındaki mesafe, mesafenin bir ucunda \(M\) var, fakat diğer ucunda bir cisim yok. Bu tanıma göre, \(M\) ile \(m\) arasında bir çekim yok, çünkü bu tanımda \(m\) yok. Tabii, bu bir tanım, bir oran veya denklem değil, çünkü, bu ifadedeki bütün terimle sabit terimler, değişen bir değer yok.
- Modern analizle Cavendish analizinin farkı. Temel fark, Cavendish'in fizik denklemleri ve standart fizik birimleri kullanmıyor olması.
- Wikipedia Cavendish deneyi sayfasına baktım. Cavendish'ten sonra geliştirilen analizin güzel bir örneği. Önce \(G\) sabitini hesaplayıp, sonra dünyanın yoğunluğunu \(G\)'den hesaplıyorlar.
- Cavendish denklem kullanmadığı için bir "orantı sabiti" olan \(G\)'ye ihtiyacı yok. Yoksa, Wikipedia yazarının dediği gibi, "o zamanlar kullanılan birim geleneklerinden dolayı \(G\) Cavendish'in analizinde açık olarak görünmüyor" değil, hayır, Cavendish, birimli fizik denklemleri kullanmadığı için ve sadece orantılar kullandığı için, \(G\) diye bir "orantı sabiti" kullanmasına gerek yok.
- Bugünlerde fizikçiler çekilen topun eleneceğini bildikleri halde ve denklemlere ve hesaplara girmediğini bildikleri halde, Newtoncu doktrini kurtarmak için denklemlere önce topu temsil eden \(m\) harfini yazmaları sonra da elemeleri bence bilimsel sahtekarlık olarak görülmelidir. Cavendish aynı sorunu, topu matematiksel bir nokta olarak tanımlayarak çözüyor ve ağırlığın bu matematiksel noktayı çektiğini söylüyor, ağırlık topu çekmiyor, bu sebepten de Cavendish'in topu \(m\) olarak yazıp sonra da elemesine gerek kalmıyor. Newtoncu çekim masalının iflas ettiği yerlerden birisi burası.
- Cavendish kolu döndürecek çekim gücünü hesaplıyor. Fakat kolun geri döndürücü gücü kolun döndüğü açıya oranlı olduğu için, topları çeken güç kolun açısı ile değişecektir. Bu sebepten, Cavendish kolun açısının maksimum olduğu zaman telin geri döndürücü gücü neyse onu hesaplıyor. Hatta, Newtoncu güç, telin gücünü aşıp kolu bir de doğal uç noktasından daha da ileri çekiyor, ondan sonra, güçler dengeleniyor. Bu da, Cavendish'in gözlemlerine uymuyor.
- Yani eğer, F(N) > F(R) durumu oluşmuşsa ve Newtoncu güç, telin geri döndürücü gücünden fazlaysa, o zaman, bu iki güç bir daha dengede kalamazlar. F(N) mesafenin karesi ile arttığı için açı ile düz olarak artan F(R)'yi bir daha bırakmaz.
- Ancak Newtoncu çekim masallarından bu denge oluşur.
- Cavendish, ağırlıkla topun merkezleri arasındaki mesafeyi, 8.85 inch olarak sabitliyor. Pratikte, kol oynadıkça, top kendisini çeken ağırlığa yaklaşıyor ve 8.85 inch mesafe azalıyor ve çekim de artıyor.
- Kolun toplam hareketi çok az, milimetrelerle ifade ediliyor.
- Daha önce, Cavendish'in, sarkacın boyutlarını dünyanın yoğunluğunu 5.5 olarak bulmak için tasarladığını söylüyordum ama artık o kadar emin değilim. Çünkü Cavendish ilk 3 deneyi çok yumuşak bir telle yapıyor, bu telin dönemi 15 dakika, daha sonra, dönemi 7 dakika olan daha sert bir telle devam ediyor ama dünyanın yoğunluğu değişmiyor, iki telle de 5.5 sayısını buluyor.
- Cavendish analizi ile devam, "dünyanın çekimi" terimi eleniyor ve yoğunluğun hesaplandığı formülde dünyanın çekimi değil, ağırlığın topu çekimi terimi var.
- Wikipedia sayfasını okumaya başladım, yanlışlarla dolu. Ufak düzeltmeler yaptım.
- Cavendish'in Newtoncu çekim gücü anlayışı. Garip bir durum, mesafenin çekim gücü yok, olamaz; hacmin çekim gücü olamaz, yoğunluğun da çekim gücü olamaz. O zaman bu Newtoncu çekim gücü nerede? Newtoncu çekim masallarında var.
- Cavendish'in analizinde, \(R/T^2\) nerede onu bulmak istiyorum.
- Cavendish hacim birimi olarak çapı 1 foot olan bir su küresi kullanıyor. Ağırlık aslında topu çekmiyor, topun merkezinde olduğu varsayılan bir madde birimini çekiyor. Aynı madde birimini, su küresi de çekiyor ve su küresi ile dünyanın çekimi de oranlanıyor yani su küresi aynı zamanda çekim birimi oluyor. (Cavendish analiz 25).
- Dünya yüzeyine yakın bir yörüngede olan uyduların yörünge hesaplarına bakmaya başladım. Uzay istasyonu, uzay mekiği ve Vanguard-1 diye eski bir uydu. Çok basit hesaplar, \(R_0^3 / T_0^3 = R^3 / T^2\) ilişkisinden çıkıyor. Newton'un yaptığı hesaplar da Kepler Kuralının bu şekilde bir uygulamasından başka bir şey değil. R0 ve T0 biliniyor ve ya T ve R'dan biri bilinmiyor, bu bilinmeyeni kolayca buluyoruz.
- Acaba Newtoncu çekim gücünün tanımını
işe karıştırmadan dünyanın yoğunluğunu hesaplayabiliyor muyuz?
- Cavendish toplarla ağırlıklar arasındaki mesafenin sabit kaldığını varsayıyor.
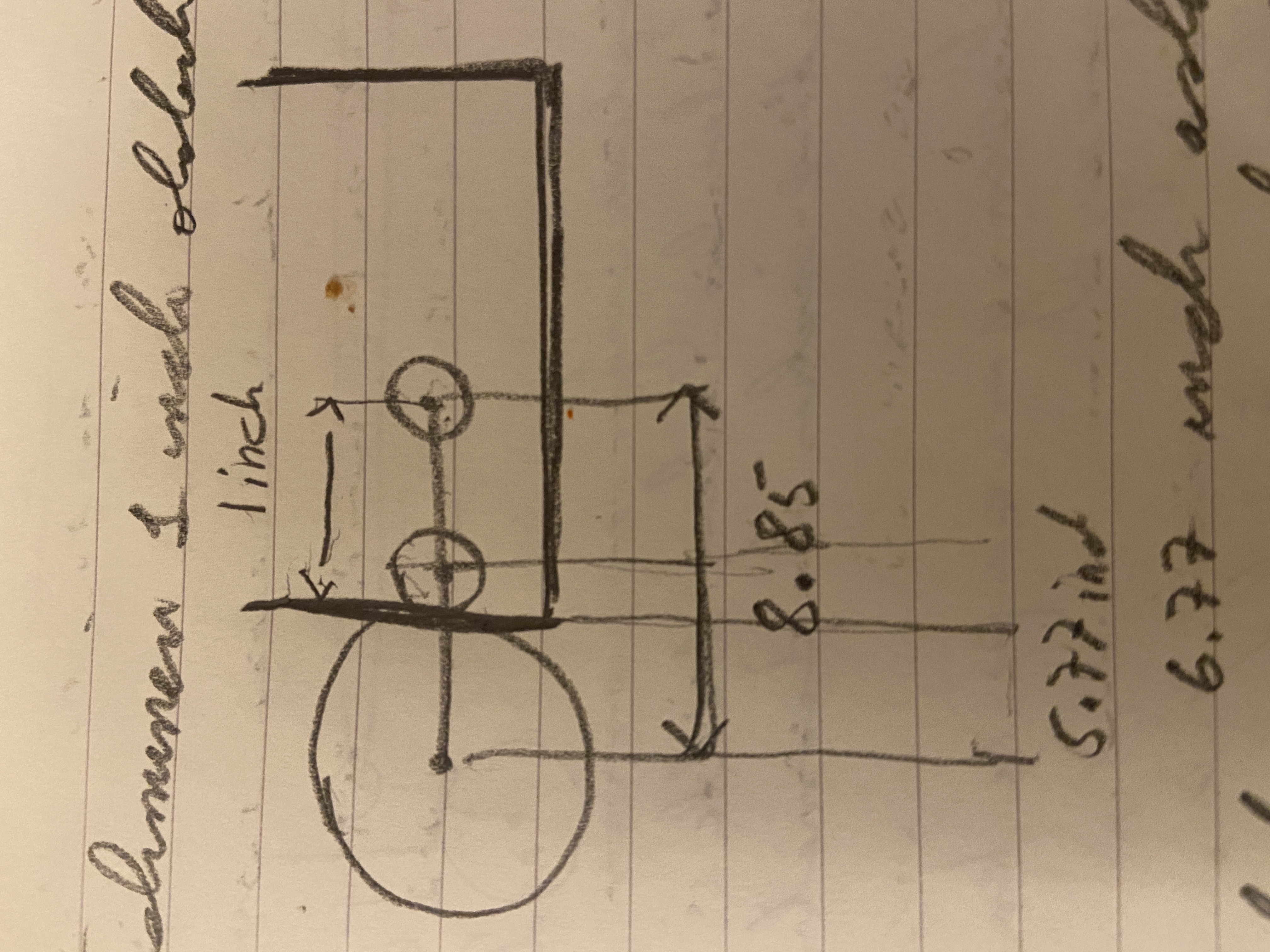
Fakat, 9. deneyde, topları kasanın kenarına kadar getiriyor bu da mesafeyi 8.85 inch'den, 6.77 inch'e düşüyor. Bu sayı kullanarak dünyanın yoğunluğunu hesapladığımızda, D = 4.58 sayısını buluyoruz, Cavendish ise 8.85'i kullanarak D = 5.29 sayısını buluyor. Fark var ama önemli değil, çünkü "dünyanın yoğunluğu" kavramı anlamsı bir kavram 5.29 da olsa, 4.58 de olsa bir şey fark etmez.
- Tercümeyi de bitirmiş oldum ama sadece deneye etkisi olan yerleri tercüme etmeye çalıştım. Gerisi sonra tamalanır.
- Cavendish bu iki gücü eşitliyor,
F(N) = F(R)
fakat, bu doğruysa, tel değiştikçe, Newtoncu gücün değerinin de değişmesi gerekir,
F(R) = F(N)
F'(R) = F'(N)
F''(R) = F''(N)
F'''(R) = F'''(N)
Fakat, Newtoncu inanca göre, Newtoncu gücün F(N)'nin eşit olduğu güç F(R) değiştiği halde kendisi değişmiyor. Bir Newtoncu mucize daha.
F(R) = F(N)
F'(R) = F(N)
F''(R) = F(N)
F'''(R) = F(N)
- Cavendish'in dünyanın yoğunluğunu hesapladığı orantıyı
şeklinde yazamıyoruz, çünkü,
\begin{align*} F(R) \propto N^2 \Rightarrow False \end{align*}Ve,
\begin{align*} \frac{F(N)}{F(1°)}= \frac{N^2}{10,683\,D} \end{align*}şeklinde de yazamıyoruz, çünkü,
\begin{align*} F(N) \propto N^2 \Rightarrow False \end{align*}çünkü Newtoncu güç F(N), sarkacın doğal dönemi \(N\) ile ilgili değil, sarkacın doğal dönemi \(N\), F(N)'den bağımsaz.
- Tercüme işine devam ettim. Cavendish bir sürü gereksiz hata olasılıklarını inceliyor ve uzun analizler yazıyor. Bu analizleri orantı matematiği ile yaptığı için çok ilginçler, ama deneyin sonuçlarını değiştirmiyorlar. Onun için şimdilik tercüme etmiyorum.
- Peki Cavendish'in "\(B\) divisions" dediği nedir tam olarak?
Bu \(B\), kolun salınımında iki uç noktanın ortasında bulunan nokta. Cavendish bu uç noktalardan bu orta noktayı hesaplıyor. Sonra, ağırlıkları bir taraftan diğer tarafa alınca, bu orta noktaya kendi çeken yakındaki ağırlığa doğru kayıyor. \(B\) kolun kaç derece Newton gücü ile oynadığı derece sayısı oluyor.
- Tercüme ile devam ettim fakat Cavendish olmayan hatalar için gereksiz hesaplar yapıyor, oraları şimdilik tercüme etmiyorum. Deney verilerini içeren tabloları teker teker giriyordum ama orijinallerin ekran resimlerini alıp onları ekliyorum
- Newtoncu analiz deneyin gerçeklerine uymuyor. Neden? Çok basit. Bu deneyde kolun hareketini belirleyen tek bir güç var, o da F(R), kolun geri döndürücü gücü. Bu deneyde, ağırlıklar ve toplar arasında bir çekim gücü yok. Peki Cavendish yaptığı deneylerde bu Newtoncu gücün etkisi altında kolun \(B\) derece döndüğünü gözlemliyor, Cavendish yalan mı söylüyor? Bunu ancak deneyi aslına uygun olarak tekrarladığımız zaman göreceğiz.
- Tercümeye de devam ettim. Cavendish ilk üç deneyi çok yumuşak bir telle yaptı, ondan sonra da teli değiştirdi ve daha sert bir tel taktı. Şimdi asıl deneylere geldik. Peki yumuşak telle hesaplanan dünyanın yoğunluğu ile sert telle hesaplanan yoğunluk arasında fark var mı?
- Cavendish deneyinde etkili olan güç çesitlerini yazdım.
- İki sayfa tercüme yaptım. Cavendish ilk üç deneyi yumuşak telle yapıyor, sonra daha sert bir tel takacak.
- Ağırlıkların asılı olduğu demir çubukların topları çekip çekmediğine baktı. Mıknatıs etkisi olsun istemiyor. Sonuçta demir çubukları bakır çubuklarla değiştiriyor ama manyetik bir durum olduğunu da tam gözlemleyemiyor. Yok yani, öyle anlaşılıyor.
- Kısa bir Cavendish analizi daha yazdım.
- Dünyanın yoğunluğu, yoğunluğun tanımından giriyor. Dünyanın yoğunluğunu bulmak için ağırlığını bilmemiz gerekiyor. Zaten ağırlığını biliyorsak yoğunluğunu da biliyoruz demektir çünkü, yoğunluk birim hacim için ağırlık demektir.
- Ama ağırlığı da zaten yoğunluk tanımından buluyoruz.
- Bir sayfa daha tercüme ettim (s.67). Artık Cavendish deneyleri anlatmaya başladı. İlk kullandığı tel çok yumuşakmış ve ağırlıklar o kadar güçlü çekmiş ki toplar, içinde bulundukları kasanın kenarlarına çarpmışlar. Cavendish çok güzel ve detaylı olarak ne yaptığını anlatıyor. Gerçekten de Newtoncu çekim gücünü yani kolun orta noktasının oynadığını gözlemlemiş mi? Yoksa sadece gözlemlediği deneyleri mi seçmiş? Bu soruları deneyi tekrarlarken inceleyeceğiz.
- Bir Cavendish analizi daha yazdım.
- Sarkaç olmadan da dünyanın yoğunluğunu hesaplayamaz mıyız?
- Tercüme ile de devam ettim
- Cavendish analizi ile devam ettim.
- Bu deneyde sarkacın rolü tam olarak nedir acaba?
- Cavendish neden çekim gücü ile telin geri döndürücü gücünü karıştırıyor?
- Cavendish analizini liste olarak yazdım.
- Analizde neden dünyanın hacmi için çap kullanılıyor diye merak ediyordum, yani dünyanın hacmi = \((41,800,000)^3\) olarak yazılıyor. Çünkü, Cavendish çapı 1 foot olan bir su küresini birim olarak alıyor.
- Bir de modern analizlerde güç değil de torque (tork, veya döndürme momenti) kullanıyorlar. Bu analizlerde, Falconer'da olduğu gibi, telin geri döndürücü torku ile Newtoncu çekim gücünün torkunu dengeliyorlar, yani eşitliyorlar:
veya,
\begin{equation*} \mu \; \frac{\theta}{2} = \frac{2 \;G \;M\; m\; a}{d^2} \end{equation*}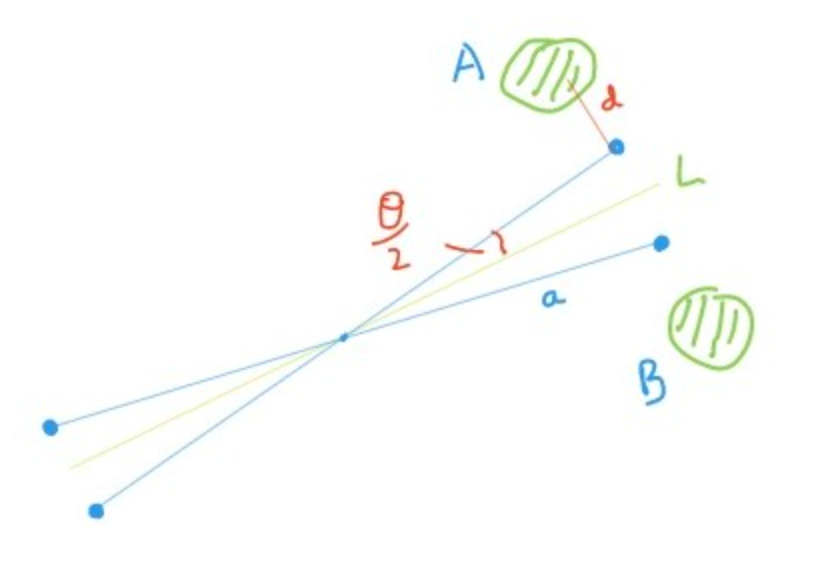
Şekil 2: Cavendish deneyi ve tork
Tork, kaldıraç yasası olduğu için, uygulanan gücün merkezden mesafesi ile gücün çarpımına eşittir. Sol taraftakı ifade, sarkaç telinin geri döndürücü gücünün torku, sağ taraf Newtoncu gücün torku. \(\theta\) / 2 diyoruz çünkü \(\theta\) sarkaç kolunun iki uç noktası arasındaki açı. \(\theta\) / 2, orta noktadan bir uç noktaya olan açısı. Sağ taraftaki 2 faktörü de, iki top ve iki ağırlık olduğu için ekleniyor.
\(\mu\) bu şekilde bulunuyor,
\begin{equation*} \mu = \frac{4\pi^2\,I}{T^2} \end{equation*}Ama Cavendish telin sertliğini, sarkacın eylemsizliğini momentini falan hesaplamıyor.
- Cavendish analiz tekrar okudum sonuç olarak Cavendish F(W)/F(E) = F(1°)/F(E) orantısını kuruyor. Yani, ağırlığın topları çekimi : dünyanın topları çekimi :: ağırlığın topları 1 derece döndüren gücü : dünyanın topları çekimi. Burada dünyanın topları çekimi terimleri eleniyor ve ağırlığın topları çekimi : ağırlığın topları 1° çekimi :: B derece ilişkisi kalıyor.
- Sayı olarak \(D = N^2 / 10,683\,B\)
- Falconer analizini tekrar okudum, bir de modern analiz veriyor, çok çirkin.
- 14. Cavendish analizi, her seferinde yeni konular çıkıyor ortaya.
- Wikipedia sayfasına baktım biraz, ama hepsini okumadım. Çok yanlışlar var. Cavendish'in yapmadığı şeyleri yapmış gibi anlatıyorlar.
- Cavendish analizini 3 bölüme ayırabiliyoruz. Cavendish ayrıca bir kaç kelime oyunu da yapıyor, telin geri döndürücü gücü ile Newtoncu çekim gücünü birbirine eşitliyor; ağırlığın topu çektiğini söylüyor ama aslında ağırlık topu değil topun merkezinde olduğu varsayılan bir madde birimini çektiğini söylüyor.
- Cavendish bir yorum daha ekledim. Cavendish kolu çeken ağırlıkların uyguladığı gücün sarkacın dönemine oranlı olduğunu söylüyor ama sonra, en son, yoğunluğun hesaplandığı ifadede görüyoruz ki, Newtoncu çekim gücü kendini, orta noktanın hareketi olarak belli ediyor, dönem olarak değil.
- Cavendish analizi ile devam. Cavendish gerçekten çok güzel bir deney yapmış ve çok da güzel bir makale yazmış. Hakkını vermek gerekir.
- Önce sarkaç kolunu oynatmak için gerekli olan gücü hesaplıyor sonra ağırlıkların topu çekim gücü ile dünyanın topu çekim gücünü oranlıyor. Sonra da kolu bir ölçek derecesi döndüren güç ile ağırlığın topu çektiği gücü oranlıyor ama bu oran sonucu dünyanın topu çekmesi eleniyor. Bunden ne anlam çikartabiliriz?
- Dünyanın yoğunluğunu hesapladığımız en son oranda \(D=N^2 / 10683 B\), dünyanın topu çekimi yok o zaman, çünkü elendi.
- Dünyanın topu çekimi dedikleri zaten topun ağırlığı. Bu konuya daha detaylı bakmak lazım, yani \(mg\). Cavendish \(mg\) olarak yazmıyor ama fikir aynı.