Cavendish sarkacın dönemini nasıl hesaplıyor?
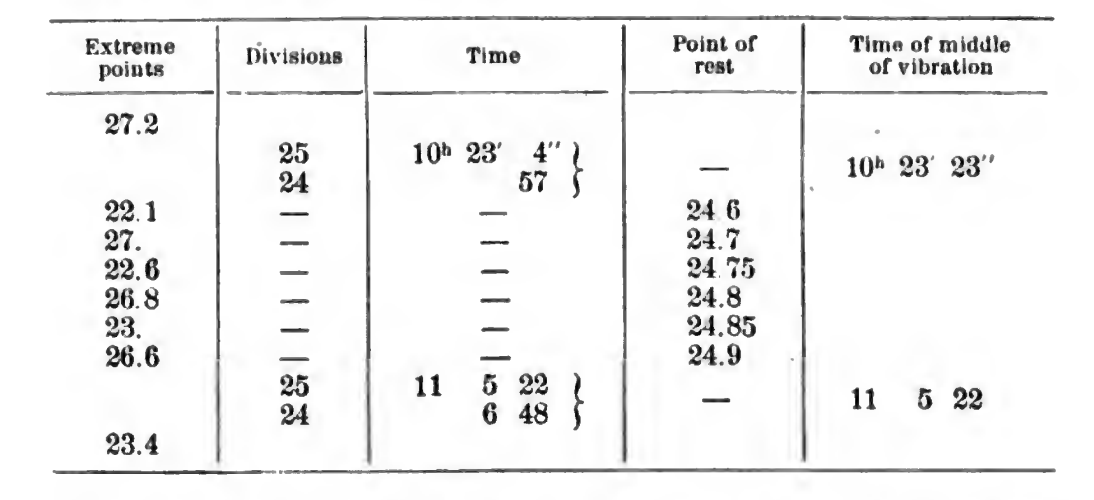
Şekil 1: Dönem hesabı
- Cavendish'in sarkacın orta noktasını ve doğal dönemini bulması lazım.
- Sarkaç kolu devamlı "kaydığı" için iki uç noktanın pozisyonundan orta noktayı bulmak iyi sonuçlar vermiyor. Cavendish orta noktayı hesaplamak için, ilk üç uç noktaya bakıyor, yani (1), (2), (3) noktalarına. (1) ile (3) aynı tarafta, sorun (1) ile (3)'ün aynı olmaması, yani kol tam olarak başladığı noktaya gelmiyor. Cavendish'in verdiği örnekten,
(1) = 27.2
(2) = 22.1
(3) = 27.0
Bu örnekte kolun başladığı noktaya geldiğinde, 0.2 derece kaymış olduğunu görüyoruz.
- Bu sebepten, Cavendish önce (1) ve (3)'ün ortalamısını alıyor
Daha sonra da bununla (2)'nin ortalamasını alıyor, ve orta noktayı buluyor,
\begin{equation*} \frac{27.1 + 22.1}{2}= 24.6 \end{equation*}Bu Cavendish'in "point of rest" dediği nokta.
- Cavendish'in sarkacın dönemini hesaplayabilmesi için de, kolun bu orta noktadan ne zaman geçtiğini bulması lazım. Bunu da şöyle hesaplıyor: Önce orta noktanın nerede olabileceğini tahmin ediyor ve bu noktanın her iki tarafında birer nokta seçip, kolun bu noktalardan ne zamam geçtiğini ölçüyor. Ondan sonra da, oratnı hesabı ile, kolun orta noktadan ne zaman geçtiğini buluyor.
- Mesela, bu örnekte, orta noktasının iki tarafında olduğunu tahmin ettiği 24 ve 25 noktalarını seçmiş ve sarkaç kolunun bu noktalardan geçtiği zamanları ölçmüş,
25……….10:23:04
24……….10:23:57
Daha önce, bu salınımın orta noktasının 24.6 olduğunu hesaplamıştı, öyleyse, kol, 1 dereceyi 53 saniyede geçtiğine göre (25'ten 24'e 53 saniyede geçti), 25'ten 24.6'ya, 53 \(times\) 0.35 ≈ 19 saniyede geçmiş oluyor, yani,
25……….10:23:04
24.6……..10:23:23
24……….10:23:57
- Aynı hesabı, 6 salınım sonrası için de yapıyor ve orta noktanın 11:05:22'de geçtiğini görüyor, ve 41 dakika 59 saniyede 6 salınım gerçekleştiğine göre 1 salınım 7 dakikada gerçekleşmiş oluyor.
- Burada incelemek istediğim bir şey daha var. Kol Newtoncu çekime göre kayarken, dönem nasıl etkileniyor? Bu ikisinin birbirinden bağımsız olması gerekir.
- Ama öte yandan, Cavendish, ilk üç deneyi yumuşak bir telle yapıyor, geri kalan deneyleri ise, daha sart bir telle yapıyor, sarkacın dönemi, 15 dakikadan, 7 dakikaya düşüyor, ama buna orantılı olarak \(B\) de değişiyor ve iki tel için de dünyanın yoğunluğu aynı kalıyor. Cavendish dünyanın yoğunluğu \(D\)'yi bu orantıdan hesaplıyor,
Öyleyse, \(N\) ile \(B\)'nin birbirlerine bağlı olması gerekmez mi?